Category: ideas
rana viam artwork
There is a general math-related puzzle called the frog hop problem. I first heard about it from watching a Stand-up Maths video. What interested me most was trying to visualize the whole thing – to create a piece of art based off of a specific set of branching decisions. The artworks here all relate to…
metatronic artwork
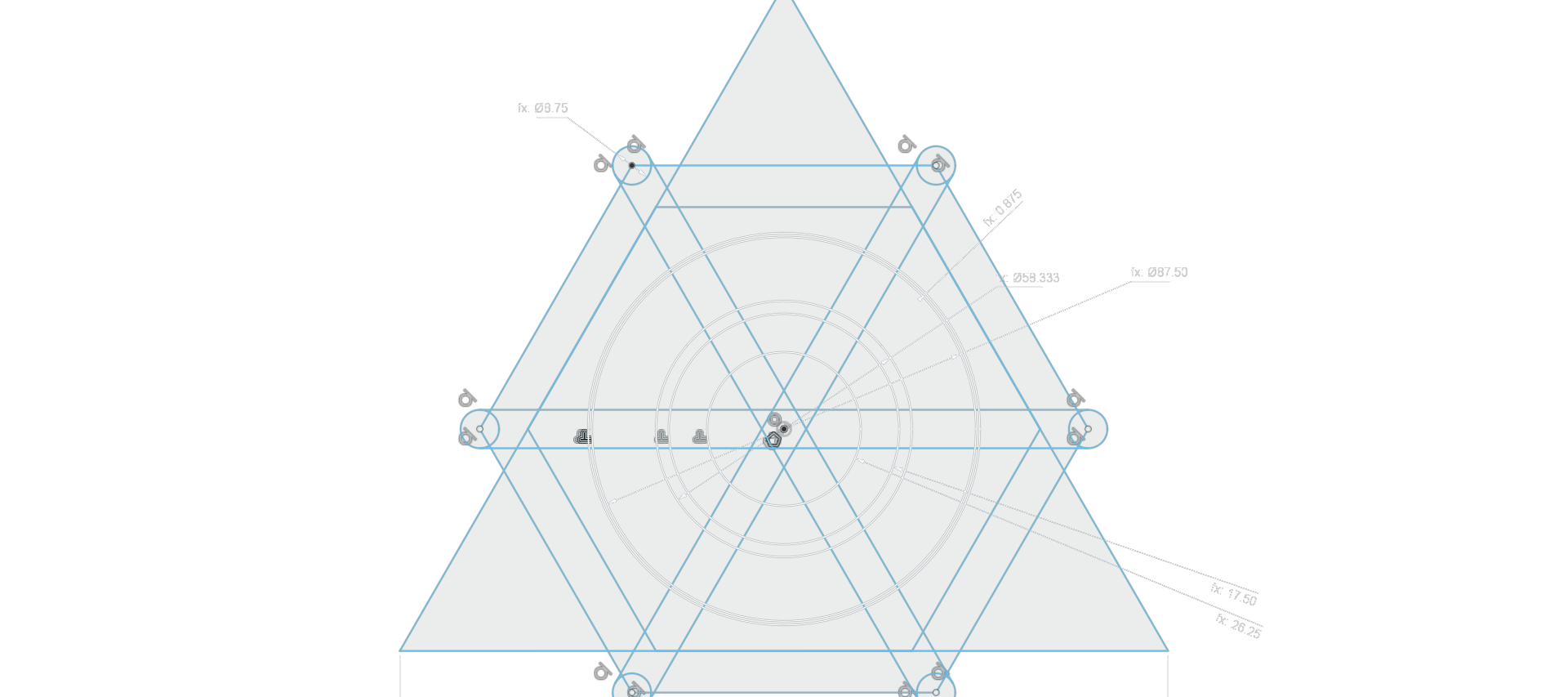
how can multiple lines pass through the centers of polyhedra and form a knot, so that each face is identical?
dead temple visions artifact lattice shirt
the official garment to accompany any Dead Temple Visions artifact
dead temple visions sculpture artifacts
a sculpture with several iterations, made for the Dead Temple Visions sound film
surface-tiling curves
semi-technical description and examples of a new way to use space-filling curves
metatronic solid face (hexahedron)
A single shape shows four negative paths curving around the center where they would otherwise intersect.
metatronic solid (hexahedron)
Four lines make a reversed knot pattern covering all faces of a hexahedron, regardless of rotation (this same pattern can tile a plane).
exploded hexahedron tiled with a plane-filling curve
A single line bisects a hollow cube into two mirrored sections.
reversed metatronic solid (hexahedron)
how to create a piece of art that you can see from all angles?
metatronic solid (tetrahedron)
Three lines make a reversed knot pattern covering all faces of a tetrahedron, regardless of rotation (this same pattern can tile a plane).
