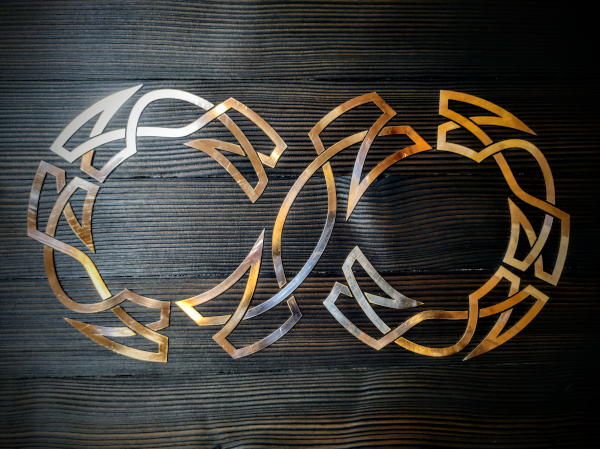Category: exhibitions
The exhibitions here are either solo or duo shows, the most recent listed first. (Artworks in group shows or smaller events are indicated on each piece’s page.)
-
surface-tiling curve hexahedron set (И 1-4)
a set of cubes surfaced with four iterations of a surface-tiling curve
-
surface-tiling curve (alternating iteration) construction diagram
a process diagram for the alternating iterations of surface-tiling curves
-
triangle tile-based surface-tiling curve listing band (И 3)
scaled listing band with surface-tiling curve segments
-
triangle-based surface-tiling curve segment intersection
splined variation of an octahedron’s surface-tiling curve
-
encompassed surface-tiling curve segment
surface-tiling curve segment resembling a certain piece of local architecture
-
surface-tiling curve deltahedron set (И 3)
folded, regular deltahedra tiled with the same curve segment
-
negative single twist components
A helix and a hexahedron are both composed from a single component, a negative single twist knot.
-
perspective hex
Eight knotted hexagons cover the surface of a cube in a pattern which is identical on each face of the solid.
-
branching unknot
Two unknots are arranged vertically above a charred wood base. The shape of the metal makes self-supporting convex and concave arrangements possible.
-
woven tile hexahedron
Copies of a single metal tile are woven together to form a cube with a concave vertex.
-
metatronic solid face (hexahedron)
A single shape shows four negative paths curving around the center where they would otherwise intersect.
-
isometric hex knot
Outlined knot segments are inlaid with copper wire. Each segment follows a path which eventually returns to its origin.
-
exploded tetrahedron divided by surface-tiling curve И 1
a surface-tiling curve slices a tetrahedron into two identical folded shapes
-
layered multi polygon knot
A group of three similar polygons rotate to form a knot. Multiple glass layers show colors, the knot itself, and a faint outline.
-
metatronic solid (hexahedron)
Four lines make a reversed knot pattern covering all faces of a hexahedron, regardless of rotation (this same pattern can tile a plane).
-
tri angle polygonal knot
A parallelogram and a triangular line rotate to create an overall triangular shape.
-
knot tiling triangle-faced polyhedra
A single shape tiles the faces of all three equilateral triangle-faced regular polyhedra with knots.
-
exploded hexahedron tiled with a plane-filling curve
A single line bisects a hollow cube into two mirrored sections.
-
tile hexahedron
A shape with interlocking edges tiles a plane. The edges of these planes bend to form a hexahedron.
-
unicursal spiral tercet
Intersecting spirals become one line. The line can be traced from any point back to its origin.
-
reversed metatronic solid (hexahedron)
how to create a piece of art that you can see from all angles?
-
metatronic solid (tetrahedron)
Three lines make a reversed knot pattern covering all faces of a tetrahedron, regardless of rotation (this same pattern can tile a plane).
-
self-intersecting tercet knots with encompassment
Three triangular twists are abound together by an encompassing shape echoing the group’s perimeter. The way the paper is cut and overlapped gives the illusion that each of the four main components are made of single pieces of paper. You have to cheat a little to give the illusion of self-intersecting lines made out of a…
-
encompassed unicursal tercet knot
A hexagonal ring bound to another triply-twisted ring is suspended vertically.
-
projected isometric tercet knot
This is a double-lined, triple-component knot based on an isometric grid. The rules of knot making are slightly bent with the double line, but half the fun of making your own system is breaking its rules. It is “projected” is because its construction uses small wooden dowels to lift the individual pieces above the surface.…
-
unicursal pentad knot
Follow the (implied) line with your eye. The line is unicursal, meaning there’s only one line. At first you might be tempted to assume there are five sections, and of course there are, but the radial symmetry is just a property of this particular line. These are probably the most difficult knots to design because…
-
tercet knot progression with self-similar encompassment
knots entangled with smaller versions of themselves
