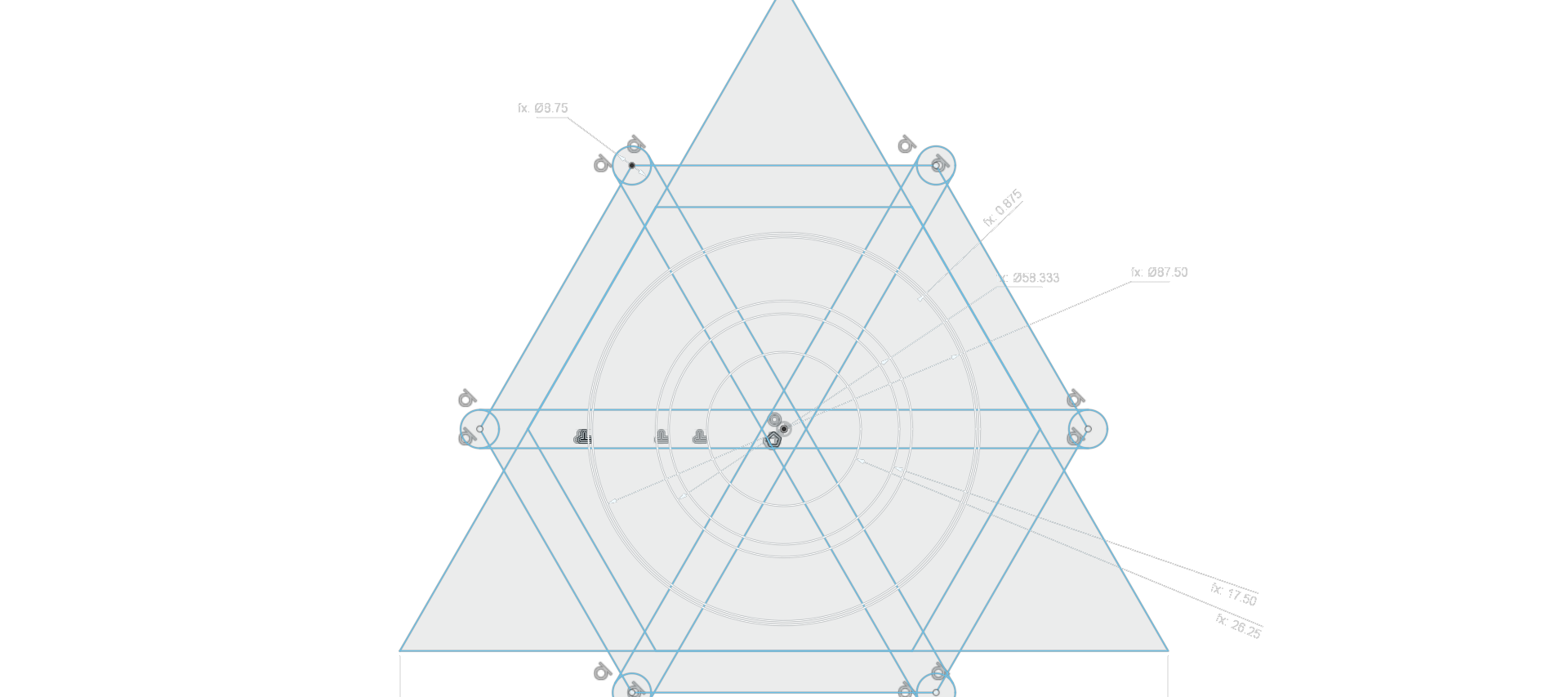
These pieces are based on the problem: how can multiple lines pass through the centers of polyhedra and form a knot, so that each face is identical? The first part of this problem is: what happens when multiple lines intersect in a knot diagram? The answer to this is that it becomes a mess, so the easiest way to avoid multiple crossings in one spot is to have crossings subsequent to the first one simply dodge the intersection. This creates the arcs in the artwork. For lines to pass through the face centers they have to start out at certain points on the perimeter. They can’t meet at the vertices or you would have another mess.
The name comes from a figure in Jewish mythology: מטטרון. An archangel and scribe, Metatron is associated with a diagram called “Metatron’s Cube,” a graph-like diagram which sort of represents the five Platonic solids, and maybe a tesseract. Upon close examination, the diagram becomes less meaningful from a math point of view. However, the idea of an angel using part of his soul to create a topological diagram is pretty epic. Additionally, I like the reference to ancient Jewish lore better than to ancient Greek math.